競馬で最適な賭け金額を見極める

競馬での賭け方を工夫すれば、限られた予算でリスクを抑えながら勝つ確率を上げることができます。特に注目すべきが、数学的根拠に基づく「ケリーの公式（Kelly Criterion）」です。この公式は、予算に対して最適な掛け金額を決めるための手法であり、元々は投資の分野で用いられてきました。競馬の予想を楽しむ皆さんにとっても、この公式は一見の価値があるでしょう。

ケリーの公式とは？

ケリーの公式は、1950年代にアメリカの数学者ジョン・L・ケリーによって考案されました。この公式は、リスクを最小化しつつ期待値を最大化するために、賭けるべき「最適な割合」を示してくれるものです。

ケリーの公式の計算方法

ケリーの公式は、以下の式で表されます。

この計算を行うと、最適な賭け金の割合が得られます。

具体例で理解する。

ある馬が勝つ確率が40％（p=0.4）と予想し、その馬のオッズが3倍（倍率が3倍ということは、賭けた金額の2倍が利益として返ってくるため、b=2）だとします。この場合、ケリーの公式に当てはめると、次のようになります

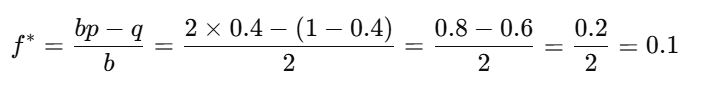
この結果、「全予算の10％を賭けるのが最適」 ということが分かります。
たとえば、予算が10,000円ある場合、10％は1,000円になります。このため、このレースでは1,000円を賭けるのがケリーの公式に基づく最適な掛け金になります。

どうして10％が最適なのか？

ケリーの公式で求めた賭け金額は、次の点で「最適」だと言えます。

• 資金の成長を最大化：10％を賭けることで、勝つと資金が効果的に増える一方で、負けた場合の損失も抑えられるため、長期的に資金が最大化されるようになっています。
• 破産リスクの最小化：仮に10％以上の賭け金を投入してしまうと、一時的な負けが続いたときに資金が大幅に減少し、最悪の場合は破産するリスクが高まります。しかし、ケリーの公式で出た「10％」というのは、破産リスクを抑えつつ、期待値がプラスである賭けを続けていくのに適切な割合なのです。

なぜ「10％より多い賭け金」ではダメなのか？

もし、ケリーの公式が出した10％よりも多く（例えば20％や30％）の賭け金を投入してしまうと、短期間で大きな利益が出る可能性もありますが、負けたときの損失が大きくなり、資金が急激に減るリスクも増します。ケリーの公式では、この「賭け過ぎのリスク」を避けるために、最適な掛け金割合を計算しているのです。

逆に「10％より少ない賭け金」ではどうなるか？

10％より少ない賭け金（例えば5％や1％）だと、リスクはさらに減りますが、資金の増え方が遅くなり、長期的に資金を効率よく増やす効果が薄れてしまいます。勝つ可能性が高い賭けに対しては、適正な割合を賭けることで効率的な成長が見込めるため、ケリーの公式で出た10％が「最適」と言えるのです。

ケリーの公式と「増えすぎず、減りすぎない」戦略

競馬やギャンブルでは、勝率が100％ではないため、勝ったり負けたりが続きます。このため、ケリーの公式は「予算の適切な割合」を賭けることで、負けてもすぐに取り返せるような賭け金を設定しています。この増えすぎず、減りすぎない絶妙なバランスが、ケリーの公式が提示する「10％」なのです。

競馬の予想モデルへの応用

ケリーの法則を使用するにあたっては勝つ確率がわかってないといけません。
python(lightGBM)で作成した予想モデルであれば、ケリーの法則を活用することができます。
例えば、1着を予想する予想モデルを作成します。予想モデルのテストでそのモデルの適合率(１着であると予想し実際に１着であった割合)を確認します。この適合率は、そのモデルで１着と予想された馬の勝つ確率と同意になります。
ケリーの公式は以下のように予想モデルに適用できます。

これにより作成した予想モデルで競馬を行う時に、最適な掛け金額を算出することができます。